An extended definition of the term "Context-free Grammars".
This was written for my Technical Writing course as a useful resource for budding linguists or computer scientists, especially those interested in programming language and compiler theory.
This definition provides a basic introduction to what context-free grammars are and how they can be used. There are some interesting computer science applications that could be discussed, but they are not included for the sake of brevity and keeping this approachable to a wide audience, especially new linguists.
By reading this definition, you will learn just what context-free grammars are, how they specify a language's rules, how you can apply these rules to a sentence in a language and visualize that application, why grammars are useful in practice, and finally some of the shortcomings of grammars and what they cannot do for us. With this definition in your toolkit, if you are so interested, you should have no problem reading basic research papers about context-free grammars, especially from the days when they were first introduced, or finding ways to use them in your projects.
As a computer science student with a strong interest in compiler theory, I enjoyed learning about this term and re-explaining it. I had to think back to when I was first learning the subject and determine what was important to know, what wasn't, and what I wish I had been taught but wasn't. The book Crafting Interpreters, which I have cited at the bottom of the definition, provided my introduction to the term and was very useful in writing this.

What are Context-free Grammars?

Context-free grammars, occasionally known as phrase structure grammars, are sets of rules that govern a language’s grammar. They apply to natural languages such as English or Spanish, but also to programming languages such as C or Java. They ensure that nouns and verbs are in the right spots relative to one another, that they aren’t in the wrong spots, that sentences end with punctuation, and enforce other language constraints. Given a grammar and a phrase that follows the grammar’s rules, the grammar derives or generates the phrase.

Definitionally, a context-free grammar consists of four different things

• V: a set of variables or “nonterminals” that will be successively replaced and eventually reduced to terminals according to the grammar’s rules
• Σ: an alphabet, or set of “terminals” generally representing letters, words, or other basic language units
• R: the set of rules that maps nonterminals to zero or more replacement sequences, which may be empty, of terminals and/or other nonterminals
• S: the start nonterminal from parsing a phrase’s grammar begins; for example, a grammar that parses sentences would likely set `S`` to whichever nonterminal represents sentences

Usually it suffices to write the rules in R to specify a grammar, with S inferred from context.

Examples of Context-free Grammars

While knowing the technical definition of a context-free grammar is great, it doesn’t do much for illuminating how they actually work and are applied. So let’s see an example! Below is a grammar that represents a simple English phrase in which a noun performs an action:

Phrase ⇒ Noun-Phrase Verb-Phrase
Noun-Phrase ⇒ Adjective Noun-Phrase | Noun
Noun ⇒ apple | bird | phone | ...
Adjective ⇒ red | happy | large | ...
Verb-Phrase ⇒ Adverb Verb-Phrase | Verb
Verb ⇒ flies | types | calls | ...
Adverb ⇒ quickly | loudly | often | ...

This is a specification of the rules in the grammar. On the left side of each rule is a nonterminal. The arrow separates each nonterminal from its possible replacements. On the right is a sequence of possible replacement sequences, separated by a pipe. An ellipsis indicates that there are many other words that follow the specified rule. Nonterminals are bolded, terminals are not.

Derivations

Let’s derive the phrase “large red bird quickly flies”. Below is the derivation. On the left is the current sequence of terminals and nonterminals. On the right is the rule used to get from the previous sequence to the next. The derivation stops when there are no nonterminals left.

Parse Trees

Given a context-free grammar and a phrase that follows its rules, it is possible to create a tree diagram that shows how each letter, word, or other unit is situated within the phrase as a whole, what type of grammatical element it is, and how to derive the phrase from the grammatical rules of the language. Below is a parse tree representing the derivation from the example above.

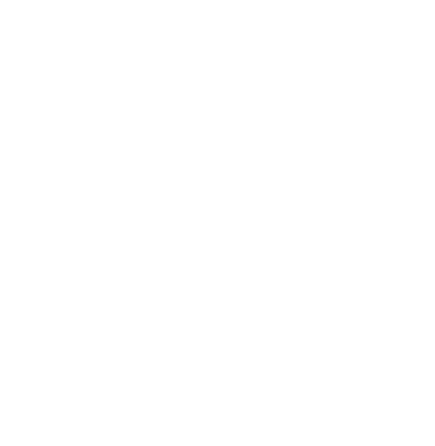
Here, it is plain to see the derivation steps that were followed to derive the final phrase from the original Phrase nonterminal. It shows how the Noun-Phrase nonterminal was replaced three separate times and what words it eventually derived into.

Applications of Context-free Grammars

All too often, it becomes easy to get lost in theory and forget that things do have useful, real-world applications. Context-free grammars are no exception! They arise in linguistics of course, but also natural language processing and programming language design. More surprisingly, they can be applied to models of computation and represent the rules for various scenarios. This explanation focuses specifically on applications to programming languages.

Programming Language Design

Context-free grammars are indispensable for validating and understanding the structure of program code. During the “parsing” phase, a compiler will apply a grammar to the input code to extract and validate meaningful structure from the input code.

Arithmetical expressions, which arise in many programming languages, serve as a great example of the importance of context-free grammars. A grammar to represent arithmetic is shown here ¹:

Expression ⇒ Literal | Unary | Binary | Grouping
Literal ⇒ [a number e.g. 123]
Unary ⇒ - Expression
Binary ⇒ Expression Operator Expression
Operator ⇒ + | - | * | /
Grouping ⇒ ( Expression )

In this grammar, a mathematical expression can be a literal number, a unary expression (an operator and another expression as an operand), a binary expression (an operator and two expressions as operands), or a grouping (an expression in parentheses). The only unary operator is negation. Binary operators can be addition, subtraction, multiplication, or division.

When a compiler is analyzing the code a programmer gives it, it will have to understand mathematical expressions; for instance, understand what expressions the programmer is looking to add or divide. This is just a small example; grammars can also validate that different keywords are used correctly and match up paired punctuation, such as curly braces and square brackets.

Syntax versus Semantics

While context-free grammars are useful, they do have limitations. Most importantly, they only represent a language’s syntax, or grammatical rules, as per their name, but not a language’s semantics. Syntax refers to structural requirements, so the grammar can make sure the nouns and adjectives are in all the right places. On the other hand, semantics refers to rules about meaning (e.g. what do certain adjective and noun pairs mean?), which these grammatical rules cannot capture and regulate.

A famous example of this syntax versus semantics distinction was crafted by linguist Noam Chomsky: “Colorless green ideas sleep furiously.” Below is a parse tree that shows how to parse the sentence according to the English grammar.

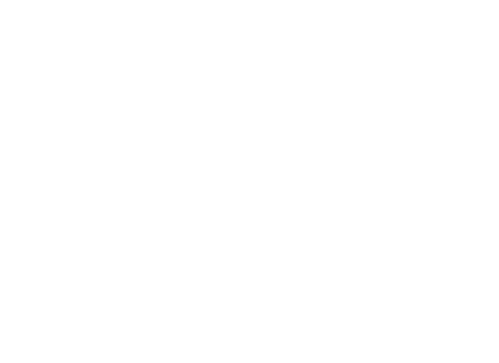
Evidently the sentence passes the syntax rules: it begins a noun phrase composed of an adjective and another noun phrase, which in itself has another adjective and the noun itself. On the other side is a verb phrase consisting of a verb and adverb to modify it. There may be additional syntax rules that could be inspected but this is enough for demonstration.

Since the grammar checks out, clearly the sentence is perfectly reasonable, right? Unfortunately, no. Try to think about what this sentence means. Can anything, much less an idea, be both colorless and green? Furthermore, how would an idea sleep? How would it do so furiously? A more figurative interpretation may be possible, but thinking of a good interpretation still poses difficulties. Evidently, context-free grammars can do nothing to prevent nonsensical sentences from arising; they only distinguish structure.

Because of this important dichotomy between syntax and semantics, context-free grammars are great for the initial stages of understanding a phrase or sentence in a language, but additional stages are required to validate and understand the meaning.

Summary

Context-free grammars are useful tools to represent the structure of languages, both natural and constructed. They consist of terminal symbols, nonterminal symbols, and rules that translate these nonterminals into sequences of terminals and/or nonterminals. A grammar derives a phrase if the phrase follows the grammar’s rules, and a derivation is the steps taken to actually generate a phrase from the grammar rules. A parse tree is a great way to visualize this derivation. Context-free grammars are vital for a wide variety of applications, including parsing programming languages. And finally, context-free grammars are not very useful for extrapolating and validating a phrase’s meaning, as a syntactically valid phrase could be semantically invalid.

Works Cited

Chomsky, Noam. “Three models for the description of language.” IRE Transactions on Information Theory, vol. 2, no. 3, 1956, pp. 113-124. IEEE Xplore, https://doi.org/10.1109/TIT.1956.1056813. Accessed 27 February 2022.

Nystrom, Robert. “Crafting Interpreters.” Crafting Interpreters, https://craftinginterpreters.com. Accessed 27 February 2022.

1. Note that there is a flaw in this grammar: it is ambiguous. In other words, there are multiple ways to group up the terminal units of a given expression. More details about that are outside the scope of this document so learning about them is left as an exercise to the reader.↩